Excel Solver (해 찾기)

Excel Solver (해 찾기) 기능을 알아보도록 하겠다.

이 기능은 '데이터' 탭에 있는데, 없는 경우 옵션에서 추가하면 된다.

옵션의 추가 기능에서 <해 찾기 추가 기능> 을 선택하고 이동을 선택한다. (나는 이미 활성화를 해서 제일 위에 있지만 활성화하지 않았다면 아래쪽에 있을 것이다. 잘 찾아보자...!) 

그 다음 <해 찾기 추가 기능>만 선택하고 '확인'을 누르면 완료!

 

"Solver" 또는 "해 찾기 추가 기능" 에 들어가면 처음 보이는 화면은 다음과 같다

 

- 목표 설정: 최대/최소로 만들고 싶은 목표셀. 함수로 되어 있어야 한다. (sumproduct 함수가 유용할 수도 있다)

- 대상: 목표를 어떤 값으로 만들고 싶은지 정하면 된다.

- 변수 셀 변경: 변수로 설정할 셀이다. 즉, 변수로 지정한 셀의 값을 변경하며 목표함수의 최적값을 찾아가는 것이다.

- 제한 조건에 종속: 제한 조건을 넣을 수 있다. 오른쪽에 '추가', '삭제' 를 활용하면 된다.

'추가'를 클릭하면 아래와 같은 화면이 나오는데, 특정 셀은 어떤 값보다 작다/크다/같다/다르다 등의 조건을 걸 수 있다.

셀을 참조할 때 드래그로 한꺼번에 여러 셀을 선택할 수 있으며, 이 경우 '셈 참조' 와 '제한 조건'의 순서가 같아야 한다.

셀에 함수가 있어도 무방하다.

- 해법 선택: 단순 LP, GRG 비선형, Evolutionary 중 하나를 선택하면 된다.

1) 단순 LP: 선형 문제일 때 단순LP 를 사용하면 된다.

목표 함수가 ax + by 와 같은 식으로 변수를 기준으로 선형이어야 한다.

!! 주의할 점: 시뮬레이션을 돌릴 때 변수가 모두 '0' 으로 설정되어 있어야 한다.

 

2) GRG 비선형: 비선형 문제일 때 GRG 비선형을 사용하면 된다.

즉, 목표함수가 ax^2 + by 또는 ax(by+c) 처럼 변수인 x, y 가 선형이 아닌 관계에 있을 때 비선형이다.

!! 주의할 점: 변수가 모두 0 으로 설정되어 있어야 하는 단순 LP와 다른게, GRG 비선형은 변수의 초기값에 따라 결과가 달라지기 때문에 변수의 초기값을 잘 선택하는 것이 관건이다. 내가 원하는 결과의 방향에 따라 초기값을 설정해주면 된다.

 

단순LP 와 GRG 는 사실 잘못 선택했을 경우 시뮬레이션 자체가 돌아가지 않기 때문에 잘못 돌릴 일은 없을 것이다.

예를 들어 해법을 잘못 선택한 상태에서 '해 찾기'를 누르면 아래처럼 '조건이 만족되지 않'았다고 뜬다.

 

- 마지막으로 음이 아닌 수로 설정할 수 있다.

 

 

이렇게 모두 설정을 완료한 후, '해 찾기'를 누르면 다음과 같은 화면이 뜬다.

- '해 찾기'를 누르는 동시에 엑셀에 변수가 목표 셀의 값이 바로 나오는데, 이 값을 유지할지, 복원할 지 선택할 수 있다.

- '해 찾기 매개 변수 대화 상자로 돌아가기' 를 선택하면 Solver 로 다시 돌아간다.

- 보고서는 3가지에 개요 보고서, 시나리오 저장까지 있는데, 우리는 '우편물 종류'(Sensitivity report) 를 보도록 하겠다.

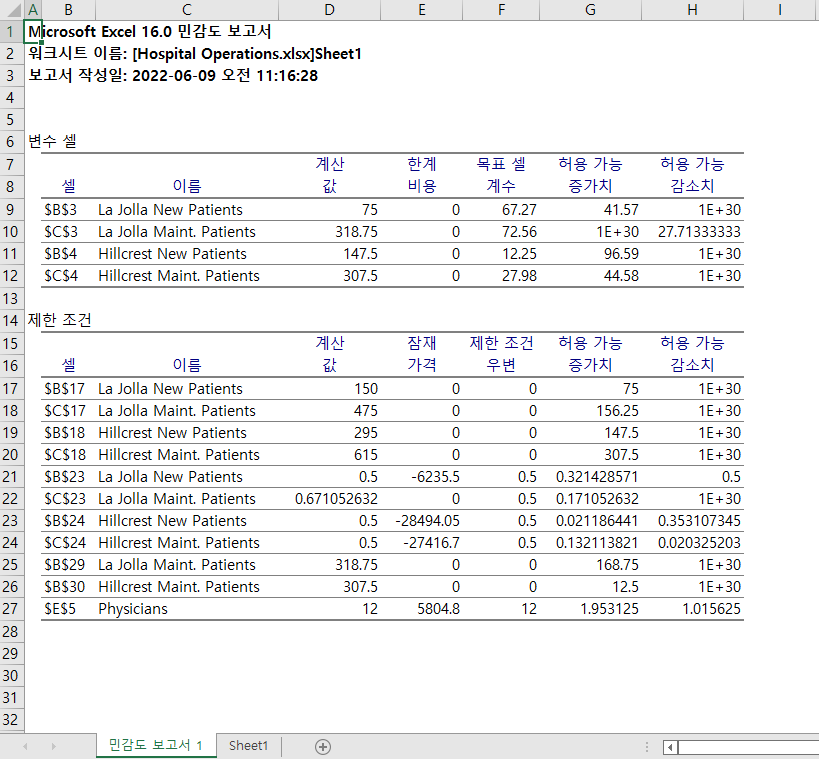
'확인' 을 누르면 아래와 같이 새로운 시트에 민감도 보고서가 만들어진다.

 

Sensitivity report (민감도 보고서) - by 우편물 종류

 

만일 엑셀이 영어로 설정되어 있다면 셀 이름이 다음과 같이 뜰 것이다.

먼저, 변수 셀(Variable cells) 를 보면, 

- 계산 값(Final Value): 최적값을 위한 변수의 최종 값이다. 

- 한계비용 (Reduced Cost): 다른 모든 조건이 같은 때, 해당 변수가 양으로 나오기 위해 계수(Objective coefficient)가 얼마나 변해야 하는지를 나타낸다. 모든 양의 변수는 한계비용 = 0 으로 나온다.

- 목표 셀 계수 (Objective Coefficient) : 말 그대로 해당 변수의 계수를 말한다.

- 허용 가능 증가치/감소치 (Allowable increase/decrease): 해당 변수의 계수가 얼마나 더 증가/감소해도 계산 값 결과가 같은지를 나타낸다. 즉, 찾은 최적값을 유지하는 한, 계수가 얼마나 증가/감소해도 되는지 허용치를 보여준다.

예를 들어, 영어로 되어 있는 보고서에서 B의 경우, 허용 가능 증가치가 3이기 때문에 계수가 5 -> 8까지 변화해도

계산 값 (Final Value) 는 유지된다.

 

제한 조건(Constraints) 부분을 보면, 

- 제한 조건 우변 (Constraint R.H.Side): 제한 조건을 설정했을 때의 값이다.

- 허용 가능 증가치/감소치 (Allowable increase/decrease): 해당 변수의 제한조건이 얼마나 더 증가/감소해도 결과가 같은지를 나타낸다. 즉, 찾은 최적값을 유지하는 한, 제한조건이 얼마나 증가/감소해도 되는지 허용치를 보여준다.

- 잠재가격 (Shadow Price): 변수가 한 단위 증가했을 때, 목표값이 얼마나 변하는지를 보여준다.

예를 들어, 영어 보고서에서 Mixer time 은 만약 75만큼 감소했다면, 목표값은 500 - 0.533 * 75 로 변화할 것이다.

그러나 non-binding 이면 (계산 값이 제한 조건과 같지 않을 때) 잠재가격 = 0 이다.

예를 들어, 영어 보고서를 보면, Butter demand = 40 < 90 이어서 non-binding 이고 shadow price = 0 이다. 즉, butter demand 의 변화로 목표값의 변화는 없을 것이다.

단, 잠재가격은 허용 가능 증가/감소치의 범위 내에서만 같은 가격을 유지한다.